GEOMETRIA: classe seconda
i poligoni
ANGOLI DI UN POLIGONO
Angoli interni di un poligono (in giallo) = angoli compresi tra due lati consecutivi
LA SOMMA DEGLI ANGOLI INTERNI DI UN POLIGONO E' : Si= 180° x (n -2)
n= numero dei lati, Si= somma angoli interni
Angoli esterni di un poligono (in blu) = angoli compresi tra un lato e il prolungamento di un lato ad esso consecutivo.
SOMMA ANGOLI ESTERNI = 360° per qualunque tipo di poligono
un angolo interno e il suo corrispondente angolo esterno, essendo adiacenti, formano sempre un angolo piatto (180°)
DIAGONALI DI UN POLIGONO

DIAGONALE = segmento che unisce due vertici non consecutivi

Numero delle diagonali che partono da ciascun vertice (d)
d = n - 3
Numero delle diagonali di un poligono ( D )
D = n x ( n - 3 ) / 2
esempio: pentagono n=5
d = 5-3 = 2
D = 5 x (5 - 3) / 2 = 5 x 2 / 2 = 5
PERIMETRO DI UN POLIGONO

il perimetro (P) è la lunghezza del contorno del poligono, corrisponde alla lunghezza della spezzata chiusa che delimita il poligono.
P = somma dei lati (formula generale)
P = AB + BC + CD + DE + EF + FA
DUE POLIGONI CON LO STESSO PERIMETRO SI DICONO ISOPERIMETRICI
figure equivalenti
rettangolo
parallelogramma
e........ATTENZIONE ALL'ALTEZZA.
quadrato
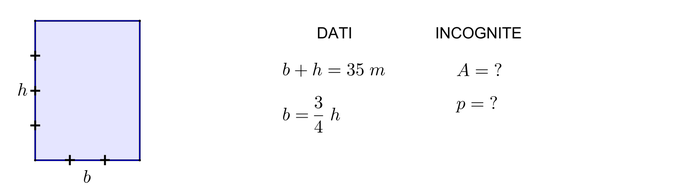
PROBLEMI DI GEOMETRIA CON LE FRAZIONI
i triangoli
LE ALTEZZE DI UN TRIANGOLO SI INCONTRANO IN UN PUNTO CHIAMATO ORTOCENTRO
dal sito: http://pitagoraeilsuoteorema.wikispaces.com/GEOMETRIA+2%5E+-+SINTESI+ARGOMENTI
LE MEDIANE DI UN TRIANGOLO SI INCONTRANO IN UN PUNTO DETTO BARICENTRO
LE BISETTRICI DI UN TRIANGOLO SI INCONTRANO IN UN PUNTO DETTO INCENTRO
GLI ASSI DI UN TRIANGOLO SI INCONTRANO IN UN PUNTO DETTO CIRCOCENTRO
LINK AD UN SITO DOVE E' SPIEGATO TUTTO MOLTO CHIARAMENTE
http://pitagoraeilsuoteorema.wikispaces.com/GEOMETRIA+2%5E+-+SINTESI+ARGOMENTI
il teorema di pitagora
LA STORIA DEL TEOREMA DI PITAGORA
VIDEO.....PER CAPIRE IL TEOREMA DI PITAGORA
il teorema di Pitagora vale solo nel triangolo rettangolo

Enunciato:
"IN UN TRIANGOLO RETTANGOLO IL QUADRATO COSTRUITO SULL'IPOTENUSA E' EQUIVALENTE ALLA SOMMA DEI QUADRATI COSTRUITI SUI CATETI"

APPLICAZIONI DEL TEOREMA DI PITAGORA.
OVUNQUE SIA POSSIBILE RICONOSCERE UN TRIANGOLO RETTANGOLO SI PUO' UTILIZZARE IL TEOREMA DI PITAGORA. ALCUNI POLIGONI SI PRESTANO PARTICOLARMENTE PER L'UTILIZZO DI TALE TEOREMA.
1) il rettangolo
tracciando una diagonale del rettangolo esso viene suddiviso in due triangoli rettangoli uguali.
Colora un triangolo rettangolo (aiuta) e utilizza il teorema di Pitagora per calcolare ipotenusa e/o i cateti in base alle richieste.

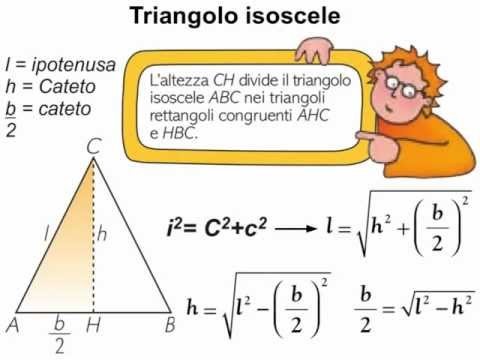
2) il triangolo isoscele
tracciando l'altezza il triangolo isoscele viene diviso in due triangoli rettangoli uguali. Colora un triangolo e in esso applica
il teorema di Pitagora per trovare il lato obliquo, l'altezza o metà base in base alle richieste e ai dati che ti sono stati forniti.

3) il rombo
il rombo viene suddiviso dalle sue due diagonali in quattro triangoli raettangoli tutti uguali.
Colorane uno e in esso applica il teorema di Pitagora per trovare la misura del lato o di una delle due diagonali in base alle richieste.

indirizzo mail: dantiscienze@gmail.com