geometria
CIRCONFERENZA E CERCHIO
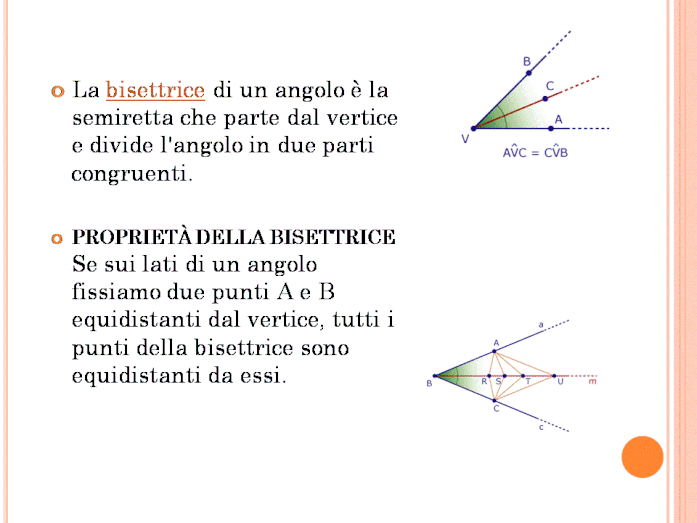
RETTA TANGENTE
è molto importante conoscere le proprietà della retta tangente ad una circonferenza
POSIZIONI RECIPROCHE TRA DUE CIRCONFERENZE
APPROFONDIMENTO: IN EVIDENZA LA DISTANZA TRA I DUE CENTRI O e O' IN RELAZIONE ALLA LUNGHEZZA DEI RAGGI r e r' (clicca l'immagine per ingrandirla)
fai attenzione ai punti in comune:
secante 2 punti in comune
tangente 1 punto in comune
interna o esterna nessun punto in comune
ANGOLO AL CENTRO: CARATTERISTICHE
ANGOLI ALLA CIRCONFERENZA: CARATTERISTICHE

RELAZIONE TRA ANGOLI AL CENTRO E ALLA CIRCONFERENZA
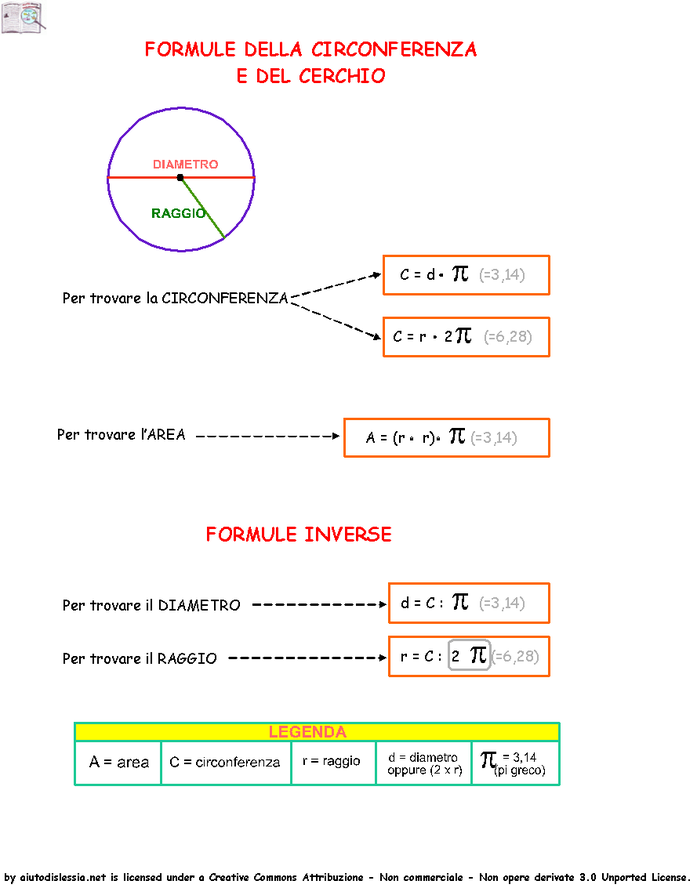
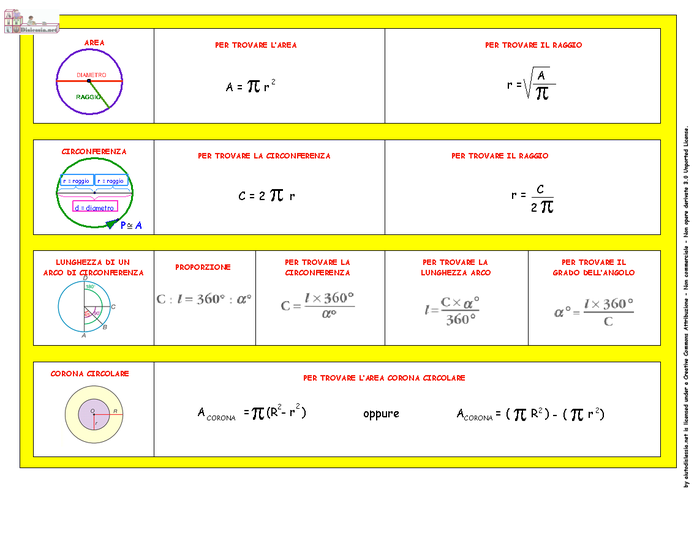
CIRCONFERENZA E CERCHIO: FORMULE
FORMULE PER TROVARE LA LUNGHEZZA DI UN ARCO UTILIZZANDO LE PROPORZIONI.
FORMULA PER TROVARE L'AREA DI UNA CORONA CIRCOLARE
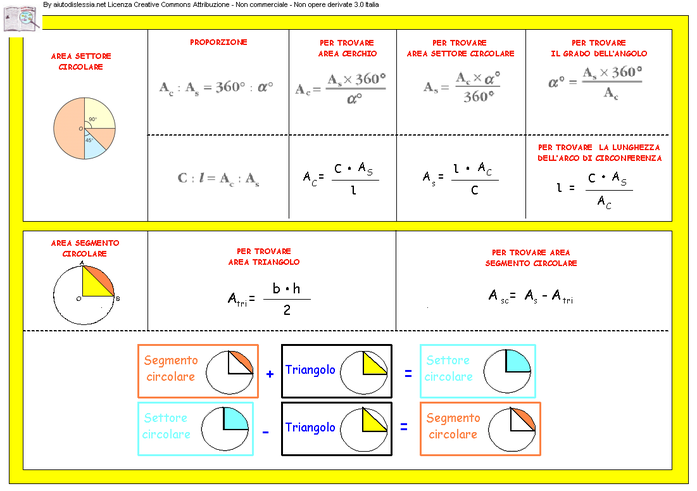
FORMULE PER LAVORARE SU UN SETTORE CIRCOLARE UTILIZZANDO LE PROPORZIONI.
N.B. GLI ELEMENTI CHE CARATTERIZZANO UN SETTORE CIRCOLARE SONO TRE: AMPIEZZA DELL'ANGOLO, LUNGHEZZA DELL'ARCO E AREA. UTILIZZANDO OPPORTUNAMENTE LE PROPORZIONI POSSO RICAVARE DI VOLTA IN VOLTA GLI ELEMENTI INCOGNITI
FORMULE PER TROVARE L'AREA DI UN SEGMENTO CIRCOLARE.
POLIGONI INSCRITTI E CIRCOSCRITTI
RIPASSO:


COME DISEGNARE UNA CIRCONFERENZA CIRCOSCRITTA O INSCRITTA AD UN POLIGONO. PRIMA SI DISEGNATE IL POLIGONO .....


UN TRIANGOLO SI PU0' SEMPRE INSCRIVERE E CIRCOSCRIVERE AD UNA CIRCONFERENZA

UN QUADRILATERO INVECE SI PUO' INSCRIVERE O CIRCOSCRIVERE AD UNA CIRCONFERENZA SOLO SE HA DETERMINATE CARATTERISTICHE.
QUINDI SE UN QUADRILATERO E' INSCRITTO O CIRCOSCRITTO AVRA' LE SEGUENTI PROPRIETA'
ATTENZIONE CIRCOCENTRO E INCENTRO COINCIDONO SOLO NEI POLIGONI REGOLARI.
ES: TRIANGOLO SCALENO
O = INCENTRO
0' = CIRCOCENTRO
i solidi
link alla presentazione completa
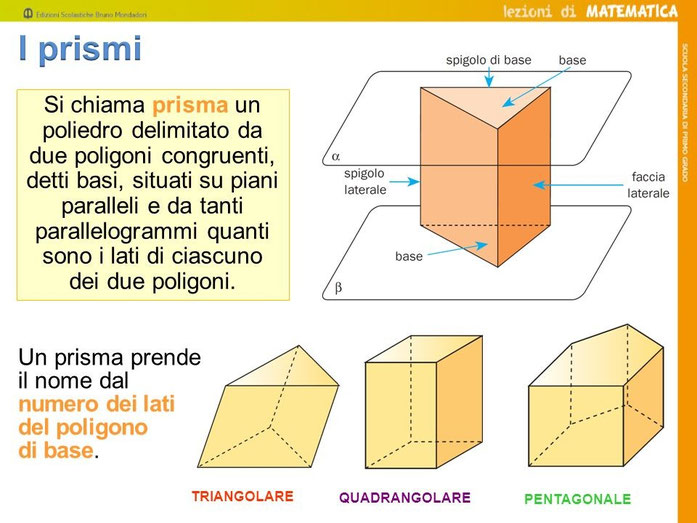
i prismi
superficie di un prisma
il parallelepipedo
il cubo
il cilindro
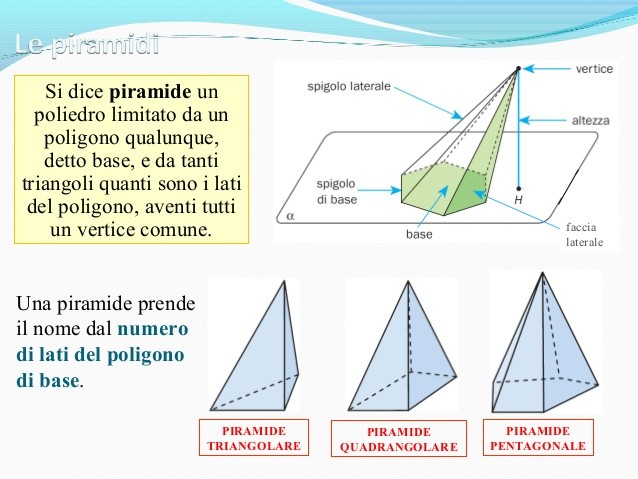
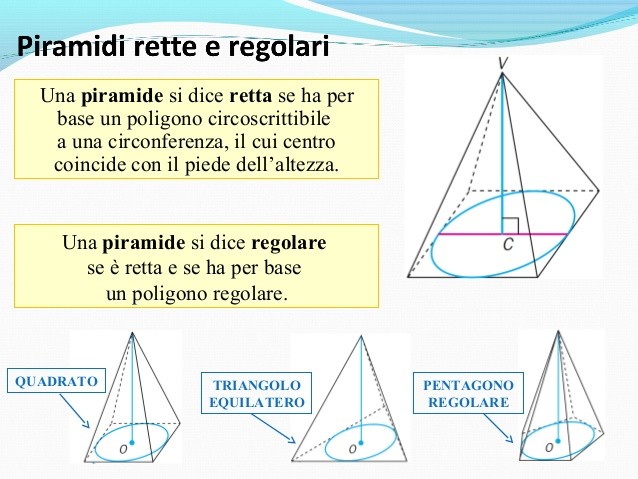
la piramide
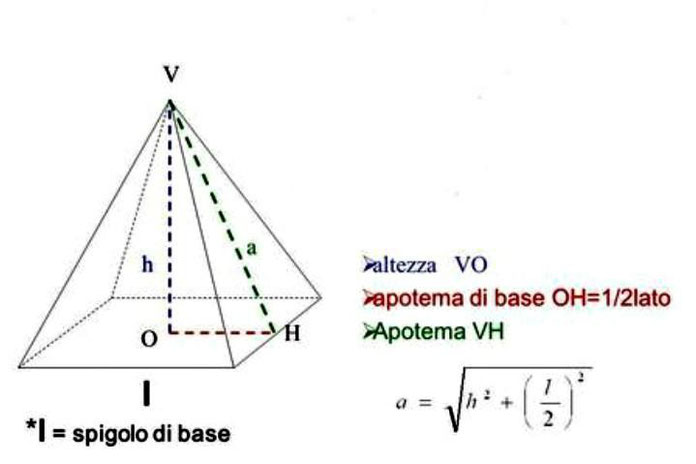
in particolare noi ci occuperemo solo della piramide RETTA A BASE QUADRATA.
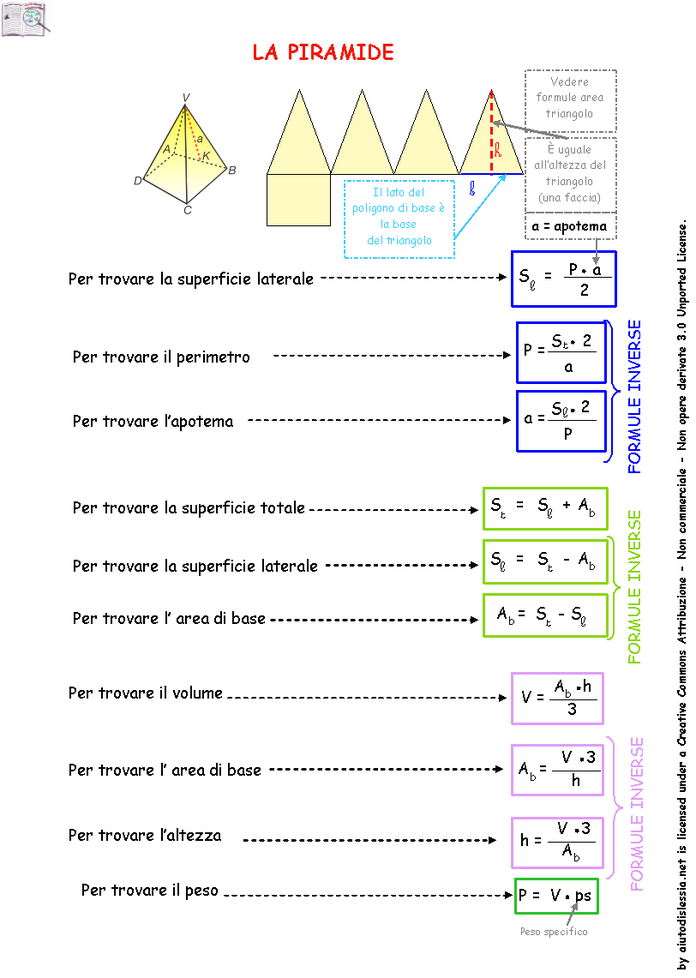
NELL'ESEMPIO SOTTOSTANTE IL SOLIDO P E' UNA PIRAMIDE RETTA A BASE QUADRATA, DI CUI POTETE VEDERE ANCHE LO SVILUPPO IN PIANO.
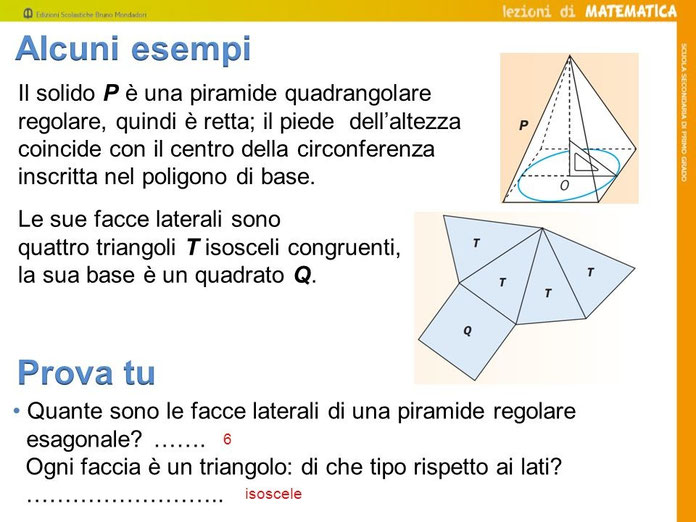
PER CALCOLARE L'APOTEMA DELLA PIRAMIDE RETTA A BASE QUADRATA SI UTILIZZA IL TEOREMA DI PITAGORA APPLICATO AL TRIANGOLO TRATTEGGIATO
SOLIDI SOVRAPPOSTI
PER CALCOLARE LA SUPERFICIE TOTALE DI UN OGGETTO COMPOSTO DA DUE SOLIDI SOVRAPPOSTI E' MOLTO IMPORTANTE CAPIRE CHE COSA BISOGNA CONSIDERARE: UN MODO SEMPLICE PER CAPIRLO E' PENSARE DI VOLER DIPINGERE L'OGGETTO.... LA SUPERFICIE TOTALE SARA' QUELLA RAGGIUNGIBILE SENZA STACCARE I DUE SOLIDI.
CASO NR. 1 : LE BASI DEI DUE SOLIDI NON COINCIDONO
OSSERVANDO IL DISEGNO CI SI ACCORGE CHE LA BASE INFERIORE DEL PRISMA PENTAGONALE APPOGGIA SUL PARALLELEPIPEDO E QUINDI ESSENDO ALL'INTERNO NON SI DEVE CONTARE, ALLO STESSO MODO UNA PARTE DELLA BASE SUPERIORE DEL PARALLELEPIPEDO, CORRISPONDENTE ALLA BASE INFERIORE DEL PRISMA, RIMANE INTERNA E QUINDI NON SI DEVE CONTARE. IN PAROLE SEMPLICI DOVRO' TOGLIERE DALLA SUPERFICIE TOTALE LE DUE BASI DEL PRISMA PENTAGONALE.
ATOT = A TOT PARALL. + AREA TOTALE PRISMA - 2 AREA BASE PRISMA.
OPPURE:
ATOT = A TOT PARALL. + AREA LATER. PRISMA
ATTENZIONE QUANDO IL SOLIDO SOVRAPPOSTO E' UNA PIRAMIDE:
A TOT= A TOT PARALLEL + A TOT PIRAMIDE - 2 AREA BASE PIRAMIDE
SOLO QUESTA FORMULA è UGUALE AL CASO PRECEDENTE.
OPPURE:
A TOT = A BASE PARALL + A LAT PARALL. + A LAT PIRAMIDE + CORNICE ( A BASE PARALL. - A BASE PIRAMIDE)
CASO NR. 2 LE BASI COINCIDONO
IN QUESTO CASO LA BASE SUPERIORE DEL PARALLELEPIPEDO E DELLA PIRAMIDE COINCIDONO E ESSENDO INTERNE NON VANNO CONSIDERATE. QUINDI:
A TOT = A TOT PARALLEL. + A TOT PIRAMIDE - 2 A BASE PIRAMIDE
OPPURE:
A TOT = A BASE PARALLEL. + A LAT PARALLEL. + AREA LATERALE PIRAMIDE
QUALUNQUE SIA IL CASO IN CUI VI TROVIATE CERCATE DI RAGIONARE INVECE DI STUDIARE TUTTI I CASI A MEMORIA.
il volume
CALCOLARE IL VOLUME DEI SOLIDI.
NON SERVE IMPARARE TUTTE LE FORMULE BASTA DISTINGUERE TRA SOLIDI A DUE BASI E A UNA BASE (ABBIAMO FATTO SOLO LA PIRAMIDE)
PER CALCOLARE IL VOLUME DEI SOLIDI A DUE BASI:
VOLUME = A BASE X ALTEZZA
PER LA PIRAMIDE:
V = (A BASE X ALTEZZA) :3
il peso
Il peso di un corpo dipende dal materiale di cui è fatto e dal suo volume. Il volume e il peso di un corpo sono grandezze direttamente proporzionali, cioè,a parità di materiale, al raddoppiare di una grandezza (il volume) raddoppia anche l'altra (il peso) e così via, e viceversa.
Ogni sostanza ha un suo determinato peso specifico, che corrisponde al peso che essa ha per unità di volume
( es. per dm3 oppure per cm3 ).
ESEMPIO : ACQUA DISTILLATA
si è visto che l'acqua distillata a 4° pesa esattamente 1 kg/dm3
la tabella seguente mette in evidenza il peso dell'acqua distillata per unità di volume nei due sistemi di misura.
CALCOLARE IL PESO DI UN CORPO
ATTENZIONE ALLE EQUIVALENZE:
IN BASE ALL'UNITA' DI MISURA CON CUI AVETE CALCOLATO IL VOLUME DI UN CORPO AVRETE UNA DETERMINATA CORRISPONDENZA DEL SUO PESO, COME EVIDENZIATO DALLA TABELLA SOTTOSTANTE CHE CONSIDERA IL VOLUME NEI DUE SISTEMI DI MISURA
IN GENERALE IL PESO SPECIFICO DI UN DETERMINATO MATERIALE VIENE FORNITO DAL PROBLEMA.
DI SEGUITO UNA TABELLA D'ESEMPIO.
IL PESO SPECIFICO VIENE SOLITAMENTE FORNITO SENZA UNITA' DI MISURA PERCHE' ESSA ANDRA' INSERITA IN BASE A QUELLA CON CUI COMPARE IL VOLUME E QUINDI CON LA CORRISPONDENZA CHE ABBIAMO VISTO SOPRA.

QUINDI UN DECIMETRO CUBO DI FERRO PESERA' 7,8 KG
UN CENTIMETRO CUBO DI ARGENTO PESERA' 10,5 GRAMMI
UN METRO CUBO DI VETRO PESERA' 2,5 MG = 2500 KG
indirizzo mail: dantiscienze@gmail.com